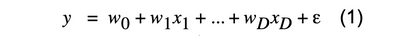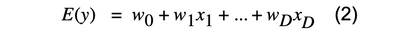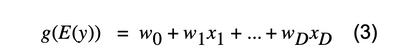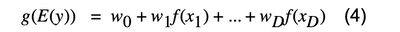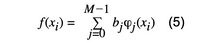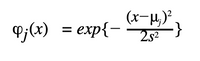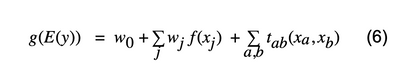線形モデル・一般化線形モデル・一般化加法モデルの関係
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
線形モデル・一般化線形モデル・一般化加法モデルの関係
データロボットでは交互作用を考慮することができるGA2Mですが、普通の線形モデルとどう違うのでしょうか。この内容を知らなくてもGA2Mを使用することはできますが、少し理解を深めていきましょう。
線形モデルから一般化線形モデル(GLM)へ
下記の式で表される回帰モデルを考えてみましょう。
εは誤差項を表します。期待値をとってノイズを取り除くと
と表現されます。ここが重要なポイントですが、回帰モデルは誤差項が正規分布に従うと仮定しています。yが正規分布に従う場合は問題ないですが、yが正規分布に従わずに歪んだ分布をしていた場合はどうでしょうか。yの分布を一般化したモデルが一般化線形モデルであり、
と表されます。例えば、yがポワソン分布の場合は関数gとして対数関数が使用されます。
一般化線形モデル(GLM)から一般化加法モデル(GAM)へ
一般化線形モデルの入力変数xに対し、一般性を持たせることはできないでしょうか。それを考えたのが、一般化加法モデルであり、
と表現されます。f(xi)を下記のような形で表現することで、さらに表現の幅が広くなります。
上記のような関数は基底関数と呼ばれています。関数f(x)は入力ベクトルxに関して非線形関数になり、表現の幅を広げることができる。式(4)はパラメータwに関しては線形なので、上記の式も紛れもなく依然線形モデルです。x2+xのような多項式回帰は、基底関数を1=x,2=x2にとった線形モデルの一例となります。
<参考>
よく利用される基底関数にガウス基底関数があります。
jは入力空間における基底関数の位置を表し、パラメータsは空間的な尺度を表します。その他、シグモイド基底関数やフーリエ基底関数もよく用いられる基底関数です。
一般化加法モデル(GAM)からGA2Mへ
GAMを用いると表現の幅がかなり広くなりましたが、GAMは変数間の関係を考慮した表現となっていません。下記の式のように、変数間の関係まで考慮したのがGA2Mです。
いよいよGA2Mが出てきましたね。GA2Mは概念としては簡単ですが、それを賢いアルゴリズムで解けるようになったのは最近の話になります。賢人の恩恵を受け、是非DataRobotでGA2Mを使ってみて下さい!
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
分かりやすい解説記事をありがとうございます!
GA2MはGAMに2因子間交互作用の項を加えたモデル、とも解釈できますね。
つまり「2因子間の組み合わせ効果」もカバーしたモデルと言えます。
2因子間の組み合わせ効果には相乗効果と相殺効果が考えられ、
- 原料Aをある温度で反応させる時だけ、反応効率がとても悪くなる(相殺効果)
- 基礎疾患×男性の組み合わせだと、同じ年齢でも疾患が急激に重症化しやすい(相乗効果)
というような例が組み合わせ効果の一例になります。
そのため、特に要因分析のケースや最終的に逆問題を解いてパラメータの最適化を行いたいというケースでは2因子間交互作用を知りたい、というニーズが高いと思います。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
@IJICHI_DR 素朴な疑問で2因子間交互作用とよく話しますが、3因子間交互作用ってどれくらいの確率で影響が出てくるものなんでしょうか。もちろんドメインによるかと思いますが、皆さんの経験をこの場でも聞ければと。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
ソフトウェアテストに実験計画法のスキームを利用して組み合わせ効果(複数のパラメータがある値をとるときだけ不具合が発生する、というようなソフトウェアバグ)を検出する方法を調査していたときに、NISTのソフトウェア組み合わせテスト(Combinatorial Testing for Software)について書かれた下記ページを参考にしていました。
https://csrc.nist.gov/projects/automated-combinatorial-testing-for-software
ホームページにチャートが掲載されていますが、これは当局に報告があったクリティカルなソフトウェアバグがいくつの因子の交互作用によるものだったかをレビューし、累積チャートにしたものです。
例えば「FDA」は医療機器に関する例になりますが、2因子間交互作用までで、クリティカルなソフトウェアバグの95%以上がカバーされていると読めます。これは私が医療機器メーカーの開発部門にいたときの実感と一致します。
一方で、数少ない3因子間交互作用が非常にクリティカルなバグだったことも経験しているので、なかなか難しいところではあります。したがって、DataRobotのHotSpot機能が3因子以上の交互作用についても重要な情報を提供してくれるのは非常に有用であると感じています。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
@IJICHI_DR さん、ありがとうございます!!
確かに私も前職の経験だとクリティカルバグは複数のテストを突破してもなお発生したという存在自体がレアなものなので、その時は3因子間交互作用なかには4因子間交互作用以上に当たった世界唯一のケースとかもありました。。。
元々のチェック体制などで条件を絞っているときには3因子間交互作用は重要になってきそうですね。このディスカッションで思い出しましたが確かに不正検知も3因子間交互作用でした。あれも簡単な不正はルールベースのシステムで弾かれていて、そこをすり抜けた強者がターゲットになるのが影響していました。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
@Miogawa さん、
なるほどですね。ソフトウェアが絡む異常検知タイプのテーマでは、特徴量の数が多くなければ例え横長データになっても3因子間交互作用までカバーできるように特徴量エンジニアリングをやった方がいいのかも。