- Community
- :
- Connect
- :
- Product Support
- :
- weighted RMSE definition
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
weighted RMSE definition
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
weighted RMSE definition
I believe that the weighted root mean squared error should be:
sqrt(sum((predicted-actual)^2*weight)/sum(weight))
The definition in the Datarobot documentation at
is
sqrt(sum((predicted-actual)^2*weight)/n)
Does that assume that the average weight is 1? What if it is not?
The errors that I see in my project don't seem to be right. When I calculate the errors myself using Eureqa models, I get a very different value. I'm not sure what to do about this. I'm trying to do a simple test case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
I created a simple data set with 20 data points and found a Eureqa model (which was incredibly bad for reasons I don't understand). In the selected model detail, it shows four data points:
weight w = [1.5 1.5 1 1]
independent variable x = [3 4 14 17]
target value y = [3.1 4 14 17]
Eureqa model values ym = [13.211 13.148 12.512 12.322] from ym = 13.4019 - 0.0635*x
The "surregate mean squared error" is 0.392. How do you get that from these data points?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Hi Redenton
I've reported inconvenience in documentation, it is implemented correct way you have written above.
So let's discuss the problem metrics you see and the calculations behind them. May you provide where you receive your numbers? Can you confirm the same behavior by downloading holdout predictions from the predictions tab along with weights columns, so the metric in-app and calculated by predictions differ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Thank you for getting back to me! I don't know how to calculate the error using the DataRobot holdout. But I have tested one of the formulas from Eureqa,
lgM = 1.6074 - 0.1628*L - 0.3459*lgNe,
using the entire data set I input into DataRobot and also on my own holdout set. Here are the results from Matlab where "Big" is the data set read into DataRobot and "Test" is the data set that I held back for testing. With
lgMBigPred = 1.6074 - 0.1628*LBig - 0.3459*lgNeBig;
rmseBig = sqrt( sum( wBig.*( lgMBigPred - lgMBig ).^2 ) / sum( wBig ) )
and
lgMTestPred = 1.6074 - 0.1628*LTest - 0.3459*lgNeTest;
rmseTest = sqrt( sum( wTest.*( lgMTestPred - lgMTest ).^2 ) / sum( wTest ) )
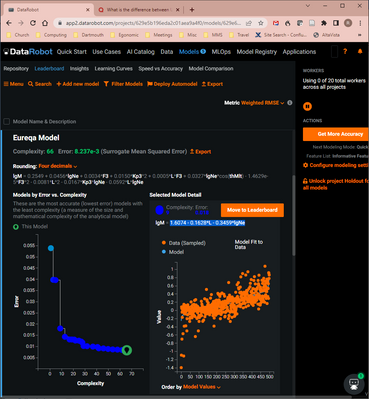
the values from this test were 0.9029 for the Big data set and 0.9135 for the Test data set. In the screen shot from DataRobot below, the error is listed at 0.018. I don't understand what that value means. Looking at the values in the bottom right plot, 0.018 seems to be much smaller than the root mean square error, regardless of the effect of the weights.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Thank you for sharing the screenshot! This is helpful to understand the problem.
The key to answering your problem here is "Surrogate Mean Squared Error" (on top of the screenshot it is defined as a metric inside Eureqa) - first it's MSE without root, second it's "surrogate", which means it's not calculated on initial data, but with some proxy data, you can read about this more here. Actual metric on the real data is shown next to the model in columns of validation\crossvalidation\holdout (depends on your partitioning setup). Also you've chosen not the best performing model, in that chain of complexities, but you can get it's real data performance by clicking "Move to Leaderboard" button, and it will show you the actual RMSE for this particular model.
But if your question is not questioning the Eureqa blueprints, but performance for any model try using actual predictions out of the model to check the metric yourself, bypassing your concerns DataRobot doing any mistakes in calculating it.
Also please let me know if anything is still confusing in-app, or documentation.