LogLossとリフトチャートの関係性について
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
LogLossとリフトチャートの関係性について
LogLossとリフトチャートの関係についてご教示いただきたいです。
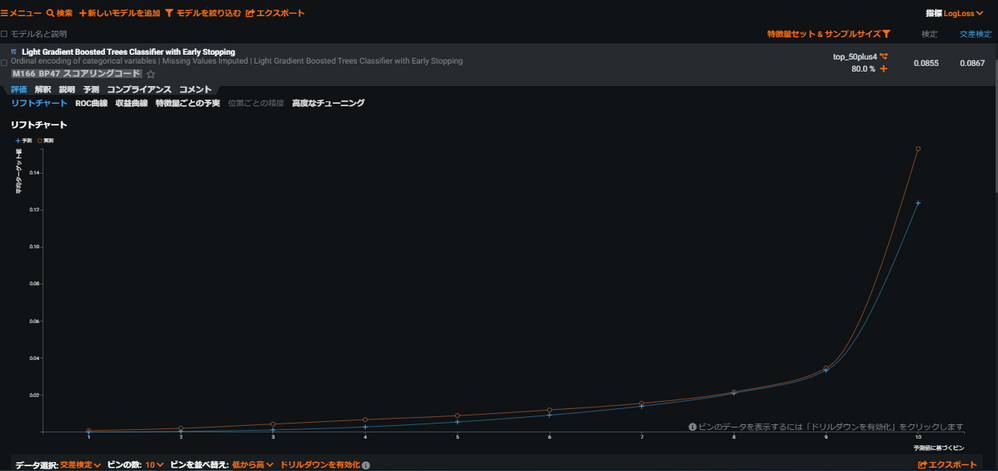
(a)特徴量のインパクト上位50変数+で作成(LogLoss:0.0867)
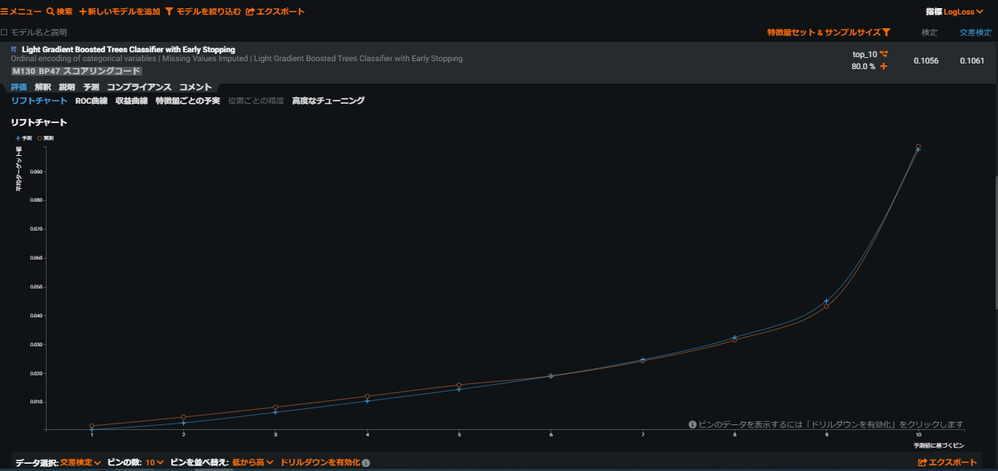
(b)特徴量のインパクト上位10変数で作成(LogLoss:0.1061)
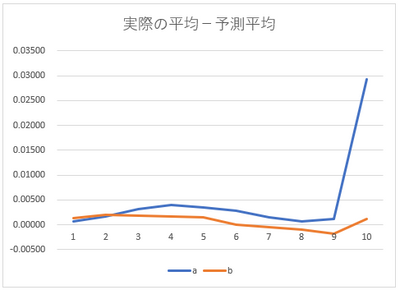
(a)(b)実際の平均-予測平均結果
LogLossが良ければ、リフトチャート上の予測実測差異は少ないように思うのですが、上記(a)(b)の結果ではそうはなっていません。本結果をどのように解釈すれば良いかご教示いただきたいです。
解決済! 解決策の投稿を見る。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
ご質問ありがとうございます。
リフトチャートを見るときに気をつけるポイントして、縦軸の「平均ターゲット率」が相対軸になるという点がございます。(リフトチャートによって縦軸のスケールが異なります。)
aのリフトチャートの縦軸はおおよそ0~0.15の幅であるのに対し、bのリフトチャートの縦軸は0~0.10になっているかと思います。
今回は2値分類だと思いますので、リフトチャートの縦軸のレンジが広いほど正負をはっきり分離できているということになります。
ですので実測と予測の重なり具合だけ見るとbのリフトチャートが良さそうに見えますが、縦軸のレンジまで加味するとaのほうが精度が良い傾向を表していると言えるかと思います。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
ちなみ今回は同一プロジェクト内でのモデル比較ですので問題ございませんが、Loglossは異なるプロジェクト(データ)に属するモデル同士を比較する際には使えない指標となります。
Loglossの話題が出ましたので、念の為補足させていただきました。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
ご回答ありがとうございます。
もう一点、リフトチャートについてご教示いただきたいです。
上記図では、実測に対して予測が下振れている傾向が全般的に見受けられます。
(特徴量ごとの作用も検定データは同様の傾向になっています)
考えられる要因としてアドバイスいただけますと幸いです。
(モデルは貸し倒れ予測モデルで、パーティション手法は層化抽出になります)
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
ご質問ありがとうございます。
予測値が下振れしているということは現在の特徴量またはモデリングで拾えていない貸し倒れパターンがあるということだと思われます。
あくまでも例ですが、貸し倒れ率が高い職業が一部あったとして、ただそれを識別できる特徴量がない場合、その職業であるために貸し倒れ率が高くなるパターンをモデルが拾えず予測が下振れしがちになることがあるかと思います。
あるいはそいういった特徴量があったとしても、傾向が著しく異なるセグメントをまとめて一つのモデルで表現しようとしているため、やはり予測が下振れするということもございます。その際はセグメントごとにデータを分けてそれぞれでモデルを作ると改善する場合があります。
DataRobotの貸し倒れ予測デモでは、年収1,000万以上の人とそれ未満の人とで貸し倒れ傾向が異なっていそうだという気づきを「特徴量ごとの作用」で確認する場面がございます。
この様に特徴量ごとの作用や、実測値と予測値の乖離が大きいデータを具体的に見ていくことで、現在のモデルで拾えていないパターンが何なのかを調べていくと手がかりがつかめるかもしれません。
ご参考になれば幸いです。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
早速のご回答ありがとうございます。
本モデルは確かに異なるセグメントをまとめて表現しようとしています。
下振れがちになるのですね。勉強になりました。
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ハイライト
- 印刷
- 不適切なコンテンツを報告
蛇足となりますが、LogLossに関してもう一点補足させていただきますと、LogLossは他のプロジェクト(データセット)で作成されたモデルとの精度比較には基本的に使えないのに対し、別の分類問題の指標でFVE Binomialというものがございます。
AUC=0.5のようなベースラインモデル(DataRobotではMajority Class Classifierというブループリントで実装されています)とのLogLoss比較した際、何%LogLossを減らせたかを表現しており、0に近いほど悪く、1に近いほど良いというようなことがAUCと同じ感じで言える指標になります。
FVE Binomial = (1 - そのモデルのLogLoss/Majority Class ClassifierのLogLoss)
ご参考まで。