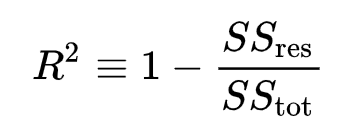- Community
- :
- Connect
- :
- Product Support
- :
- R square value different from manual calculation
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
R square value different from manual calculation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
R square value different from manual calculation
Hi ,
The following validation set and its prediction values shows an R2 value of 0.69 where as Datarobot result shows 0.65. This is not specific to this one data set, whatever model i use, when i check the validation set and calculate its R2, its slightly different from what datarobot is showing. Am i missing anything?
| Actual | Prediction |
| 17.98 | 63.6761 |
| 35.61 | 40.0788 |
| 54.16 | 79.47874 |
| 58.69 | 56.8481 |
| 77.57 | 97.33846 |
| 141.14 | 157.1376 |
| 161.05 | 106.6461 |
| 178.8 | 127.3321 |
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Hi Manojkumar and Erica,
This was a good question. I had to do some digging to find the answer 🙂
There are several methods for computing R2, and their results don’t always match. We use the most general definition of R2, which you can read about in detail on wikipedia: 1 - (residual sum of squares) / (total sum of squares):
Here is some R code that explains the calculation more thoroughly:
a <- c(17.98, 35.61, 54.16, 58.69, 77.57, 141.14, 161.05, 178.8)
p <- c(63.6761, 40.0788, 79.47874, 56.8481, 97.33846, 157.1376, 106.6461, 127.3321)
# Manual method
SSE = sum((p - a)^2)
SST = sum((mean(a) - a)^2)
R2 = 1 - SSE/SST
print(R2) # 0.6550015
# Package method
print(MetricsWeighted::r_squared(a, p)) # 0.6550015
The residual plot uses the same approach, but down samples some of the data. Specifically if there are more than 1000 data points. So you may see some differences here as well.
I hope this helps. Thanks for posting!
Emily
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Hi Manoj
There are several types of R² - in addition to the calculation that you will have learnt in school there are also:
Adjusted R² - which account for the effect of adding more fields to the data (this can "artificially" fit the data)
Predicted R² - this will directly check the prediction by rerunning the model with missing data points and checking its prediction against those points.
Both these values will be lower than the "vanilla" R² but will be more accurate. I am not sure - trying to check the documentation to see but I imagine that datarobot would use one of those metrics rather than the standard.
Erica
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Well I'm curious now :0)
@emily or anyone else from Datarobot ...
Can you tell us what kind of R squared is used in the residuals tab? It doesn't specify in the documentation. Thank you!
https://app.eu.datarobot.com/docs/modeling/investigate/evaluate/residuals.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Hi Manojkumar and Erica,
This was a good question. I had to do some digging to find the answer 🙂
There are several methods for computing R2, and their results don’t always match. We use the most general definition of R2, which you can read about in detail on wikipedia: 1 - (residual sum of squares) / (total sum of squares):
Here is some R code that explains the calculation more thoroughly:
a <- c(17.98, 35.61, 54.16, 58.69, 77.57, 141.14, 161.05, 178.8)
p <- c(63.6761, 40.0788, 79.47874, 56.8481, 97.33846, 157.1376, 106.6461, 127.3321)
# Manual method
SSE = sum((p - a)^2)
SST = sum((mean(a) - a)^2)
R2 = 1 - SSE/SST
print(R2) # 0.6550015
# Package method
print(MetricsWeighted::r_squared(a, p)) # 0.6550015
The residual plot uses the same approach, but down samples some of the data. Specifically if there are more than 1000 data points. So you may see some differences here as well.
I hope this helps. Thanks for posting!
Emily
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
Hi Emily,
Thanks for the detailed clarification !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Printer Friendly Page
- Report Inappropriate Content
r-squared refers to the 'goodness' of fit for a particular model with no regard for the number of independent variables. Whereas, adjusted r-squared takes into account the number of independent variables.
So if you have a regression equation such as
y = mx + nx1 + ox2 + b
The r-squared will tell you how well that equation describes your data. If you add more independent variables (p, q, r, s ...) then the r-square value will improve because you are in essence more specifically defining your sample data. Using adjusted R-squared metric instead takes into account that you have added more independent variables and will 'penalize' the result for the more variables you add which don't fit the sample data. This is a good way to test the variables, either by adding in one at a time and checking when the adj-R2 starts to deteriorate or by starting with all the variables and removing one at a time until the adj-R2 doesn't improve.